11. 재귀함수에 대해 설명해 주세요.
함수 본인을 내부적으로 다시 호출하면서 동일한 동작을 반복 수행하는 함수를 의미합니다.
- 장점
- 함수의 코드가 단순해집니다.
- 코드상에서 변수를 여러개 선언하지 않아도 됩니다.
- 단점
- 함수 호출 후, 이전 함수로의 복귀 과정에서 Context Switching이 발생해 추가적인 오버헤드가 발생할 수 있습니다.
- 이로 인해 성능이 반복문에 비해 느릴 수 있습니다.
- 여러개의 변수의 개수를 필요로 하지는 않지만 재귀적 호출 과정에서 계속해서 매개변수, 지역변수 등의 정보를 스택 메모리에 쌓아 메모리 소모량이 큽니다.
- 무한루프에 빠지거나 무리하게 사용할 경우, Stack의 메모리 공간을 초과해 StackOverFlow가 발생할 수도 있습니다.
무조건 반복문보다 느린가?
- 반복문보다 재귀함수가 느린 이유는 쌓이는 스택 메모리, 반복적인 계산, 매개변수나 지역변수가 재귀하는 만큼 생성되는 등의 이유가 있습니다.
- 이를 꼬리 재귀나 메모이제이션 등의 최적화를 통해 보안한다면 반복문과 비슷한 성능을 낼 수 있으면서 가독성이 좋은 코드로 구성할 수 있습니다.
- 즉, 재귀가 반복문에 비해 느려질 수는 있지만 절대적이지는 않고, 이를 해결할 수 있는 방법이 있다 정도로 이해하면 좋을 것 같습니다.
Context Switching이란?
- 멀티 쓰레드 환경에서 처리하는 쓰레드가 변경될 때, 변경되는 쓰레드에 따라 실행 상태를 변경하는 과정을 의미합니다.
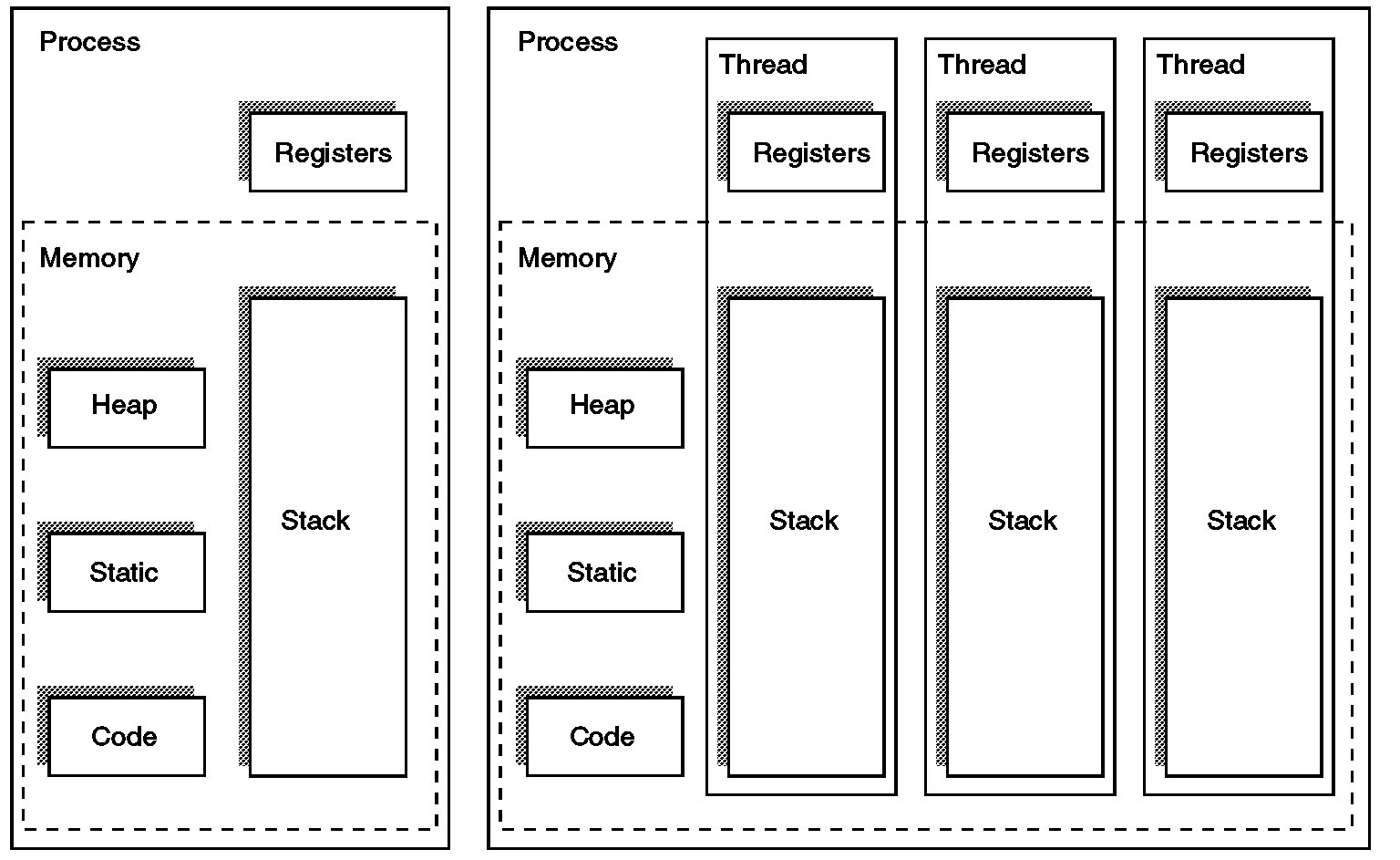
- 멀티 쓰레드 환경에서 재귀 함수는 여러 쓰레드에서 작업이 동시에 이뤄질 수 있습니다. 이 과정에서 쓰레드별로 가지는 독립적인 스택 메모리에 함수에 대한 정보가 저장됩니다.
- 이 형태에서 재귀 함수가 종료되고 이전 함수로 돌아가는 과정에서 쓰레드의 변경이 있다면 Context Switching이 발생할 수 있습니다.
이미지 참고
재귀 함수의 동작 과정을 Call Stack을 활용해서 설명해 주세요.
Call Stack은 함수 호출을 추적하는 메모리 구조로서, 함수가 호출될 때마다 해당 함수의 정보를 스택에 저장하고, 가장 마지막에 호출된 함수가 종료되면 해당 함수 정보를 스택에서 제거하면서 동작합니다. 그리고 제거된 함수 이전에 호출된 함수에서 그 제거된 함수의 결과값을 가지고 특정 작업을 처리하는 방식으로 재귀함수는 동작합니다.(스택에 저장된 정보를 역순으로 꺼내면서 반환값을 계산) 그래서 호출되는 함수가 특정 지점에선 결과값을 리턴해 연속적으로 함수를 종료하고 복귀할 수 있는 지점이 있어야 합니다.
언어의 스펙에 따라, 재귀함수의 최적화를 진행해주는 경우가 있습니다. 어떤 경우에 재귀함수의 최적화가 가능하며, 이를 어떻게 최적화 할 수 있을지 설명해 주세요.
재귀함수의 최적화란 재귀함수가 동작하는데 있어 필요한 메모리 사용량을 최소한으로 줄여주는 과정이라고 생각합니다. 이러한 최적화는 두가지 방법으로 나눠볼 수 있습니다.
- 꼬리재귀(Tail Call Recursion) (참고영상 6분부터 시청)
- 재귀함수 다음에 추가적인 연산을 하지 않도록 구현해 하나의 스택 프레임 내에서 재귀적인 동작이 가능하도록 지원하는 방식
- 재귀함수를 통해 얻어낸 최종 결과값만 리턴하고 그 전에 가지게 되는 결과값은 매개변수를 통해 전달해야 합니다.
1 2 3 4 5 6 7 8 9 10 11
public class Recursion { public int factorial_no_tail(int n) { if (n == 1) return 1; else return n * factorial_no_tail(n-1); // 재귀함수 호출 이후에 추가 연산 진행 } public int factorial_yes_tail(int n, int sum) { if (n == 1) return 1; else return factorial_yes_tail(n-1, sum * n); // 재귀함수 호출 이후에 추가 연산 미진행 } }
- 하지만 JAVA에선 직접적으로 꼬리재귀에 대한 지원을 하지 않습니다.
- 이유는 JDK 클래스에서 호출한 메소드이 개수를 알아야 하는 메소드가 있어 꼬리재귀로 인한 호출 함수를 줄이면 에러를 발생시킬 수 있기 때문입니다.
- 그래서 JAVA 8부터 람다와 함수형 인터페이스로 동일한 컨셉의 구현은 가능하다고 알고 있습니다.
- 메모리제이션(Memoization)
- 재귀 함수를 통해 얻게 된 결과값을 하나의 메모리에 저장해두고 동일한 매개변수를 통한 결과값을 도출해야 할 때, 동일한 재귀함수를 수행하지 않고 미리 저자한 데이터만 가져와 사용합니다.
- 반복적인 계산과정을 줄여나가는 좀 더 효율적인 재귀함수가 동작할 수 있는 방법입니다.
- 대표적으로 해시 테이블을 사용해 볼 수 있으며 동적 계획법과 같은 맥락으로 이해할 수 있습니다.
12. MST가 무엇이고, 어떻게 구할 수 있을지 설명해 주세요.
- MST는 Minimum Spanning Tree(최소 신장 트리)의 약자로 그래프 내에 모든 정점을 연결하면서 최소 비용으로 만들어지는 트리를 의미합니다.
- 여기서 말하는 트리는 사이클이 없는 연결 그래프를 의미합니다.
MST를 구하는 방법은 대표적으로 두가지가 있습니다.
- Kruskal 알고리즘
- 간선들의 가중치를 적은 순부터 차례대로 정렬한 다음 작은 가중치부터 차례대로 가져와 정점을 연결하는 방식입니다.
- 이 과정에서 사이클이 발생하는 시점의 간선은 제외합니다.
- 시간복잡도는 간선을 정렬하는데 O(E Log E), Union-Find 알고리즘을 통해 정점들 간의 사이클을 확인하는데 O(E Log V) 입니다.
- 간선 정렬 : 간선의 수(E)만큼 퀵정렬, 병합 정렬(Log E)을 사용해 정렬하기 때문에
- Union-find : 간선의 수(E)만큼 알고리즘을 수행하고 알고리즘에서 고려하는 건 정점의 수(Union : Log V / Find : Log V, 실제 복잡도는 a(V)로 수행시마다 달라진다.)
- 보통 E가 V보다 큰 형태인 그래프가 많기 때문에 O(E Log E)의 복잡도를 가진다고 봐도 무방합니다.
- Prim 알고리즘
- 가중치가 가장 작은 간선을 우선적으로 접근해 정점을 연결하는 방식입니다.(다익스트라 알고리즘과 비슷한 개념)
- 정렬은 우선순위 큐를 사용합니다.
- 시간 복잡도는 O(E Log V)로 계산됩니다.
- E의 수만큼 동작하며 우선순위 큐에서 V에 대한 정렬을 하기 때문입니다.
Kruskal 알고리즘에서 사용하는 Union-Find 자료구조에 대해 설명해 주세요.
- 여러개의 노드 중 두개의 노드가 서로 같은 그래프에 속하는지 판별하는 그래프입니다.
- 서로소 집합 알고리즘이라고 부릅니다.
- 순차적으로 부모 노드를 찾아가면서 그래프의 집합을 판별해 내는 역할을 합니다.
- 부모 노드를 찾아가는 과정은 재귀함수로 동작합니다.
Kruskal 과 Prim 중, 어떤 것이 더 빠를까요?
- 대부분의 경우에선 Prim이 더 빠른 경우가 많습니다.
- 이는 시간 복잡도 상으로 O(E Log V) 가 O(E Log E)보다 나은 경우가 많기 때문입니다. E가 V보다 크기 때문입니다.
- 하지만 이는 절대적인 값이 아니므로 상황에 따라 더 적합한 알고리즘을 선택해야 합니다.
- 희소 그래프(적은 간선을 가지는 그래프)의 경우, Kruskal 그래프가 더 적합합니다.
- 밀집 그래프(많은 간선을 가지는 그래프)의 경우, Prim 그래프가 더 적합합니다.
13. Thread Safe 한 자료구조가 있을까요? 없다면, 어떻게 Thread Safe 하게 구성할 수 있을까요?
몇몇 언어의 라이브러리에선 Thread Safe한 자료구조를 제공해주고 있습니다.
- 만약 제공되는 자료구조 중에 Thread Safe한 자료구조가 없다면 아래와 같은 개념을 적용해볼 수 있습니다. (참고자료)
- 뮤텍스(Mutex) : 락에 대한 키를 두고 해당 키를 소유한 프로세스만이 공유 메모리에 접근이 가능하도록 구현하는 방식
- 세마포어(Semaphore) : 공유 메모리 접근 권한에 대한 허용 범위를 지정해 해당 범위 내의 개수만큼 접근하는 프로세스의 수를 제한하도록 구현하는 방식
- 위 두 방식의 차이점
- 세마포어는 뮤텍스가 될 수 있지만, 뮤텍스는 세마포어가 될 수 없다.
- 세머포어는 소유하지 못하지만 뮤텍스는 소유할 수 있다.
- 세마포어는 여러 개의 동기화 대상을 가지며 뮤텍스는 오직 하나의 동기화 대상만을 가진다.
배열의 길이를 알고 있다면, 조금 더 빠른 Thread Safe 한 연산을 만들 순 없을까요?
- 직접적으로 빠른 연산을 만들어낼 수 있는 방법을 제공하지는 못하지 않을까
- 좀 더 고민해보기
사용하고 있는 언어의 자료구조는 Thread Safe 한가요? 그렇지 않다면, Thread Safe 한 Wrapped Data Structure 를 제공하고 있나요?
- JAVA를 기준으로 다음과 같은 자료구조들이 Thread Safe한 형태로 기능을 제공해주고 있습니다.(참고자료)
- Synchronized Collection
- Vector / HashTable / SynchronizedXXX 형태의 클래스명으로 제공되는 자료구조들
- 메소드에
synchronized키워드가 포함되어 있어, 해당 메소드 호출 시 해당 메소드를 가진 객체에 락이 걸려 다른 쓰레드가 접근하지 못합니다. - 하지만 객체 자체에 락이 걸려 상대적으로 성능이 느리며 병렬처리를 지원하지 못한다는 단점이 있습니다.
- 뮤텍스 방식이 적용된 자료구조라고 볼 수 있습니다.
- Concurrent Collection
java.util.concurrent패키지에 포함된 클래스들- 자료구조 전체가 아닌 필요에 따라 부분적으로 락을 걸어 동시성과 병렬 처리를 모두 가능하게 하는 자료구조입니다.
- 대표적인 자료구조
- ConcurrentHashMap : Lock Striping 방식을 사용해 버킷 별로 락을 설정하는 방식으로 동작합니다.
- Synchronized Collection
- JAVA에서는 Wrapped Data Structure 방식으로 Thread Safe한 자료구조를 제공하고 있지 않습니다.
- 내부적으로 동기화 메커니즘을 사용하거나 비차단 알고리즘을 사용해 스레드 안정성을 보장합니다.
- 내부적인 동기화 처리 방식 : ConcurrentHashMap, CopyOnWriteArrayList, ConcurrentLinkedQueue
- 비차단 알고리즘 : ConcurrentSkipListMap, ConcurrentSkipListSet
비차단 알고리즘(Non-Blocking Algorithm)이란?
- 전통적인 스레드 동기화 알고리즘과 달리 락에 대한 개념없이 모든 스레드가 동시적으로 자료구조에 접근이 가능합니다.
- 다만, 다른 스레드가 처리하고 있는 작업에 대해서는 영향을 주지 않도록 동작하는 알고리즘입니다.
- 이를 위해 CAS 개념을 적용해 볼 수 있습니다.
CAS(Compare And Swap) : 변경된 데이터를 공유 변수와 같은 메모리에 저장하기 전에 해당 쓰레드가 미리 복사해둔 원본 데이터와 현재 저장된 데이터를 비교해 같다면(아직 다른 쓰레드에서 처리하지 않았다고 판단) 새로운 데이터로 변경하고, 다르다면(다른 쓰레드에서 중간에 데이터를 처리했다) 처리를 하지 않는 방식을 의미합니다ㅏ.
기본적으로 Stack 영역에 저장되는 매개변수, 지역변수는 동기화에 대한 지원 필요없이 다른 쓰레드에서 접근이 불가능합니다. 이는 Stack 영역은 하나의 쓰레드에 독립적으로 위치하기 때문입니다.
private final 을 사용해 불변 변수로 생성된 경우에도 조회만 가능하기에 동시성에 대한 고려는 크게 중요하지 않다고 볼 수 있습니다.
14. 문자열을 저장하고, 처리하는 주요 자료구조 및 알고리즘 (Trie, KMP, Rabin Karp 등) 에 대해 설명해 주세요.
- Trie
- 문자열을 저장하기 위해 사용되는 알고리즘으로 이진 탐색 트리에 문자열을 저장합니다.
- 저장해야하는 문자열마다 문자하나씩 자식노드로 생성하면서 저장하는 방식으로 동작합니다.
- 데이터 저장보단 이후 탐색하는 과정에서 높은 성능을 내기 위해 사용됩니다.(M : 문자열 개수, L : 가장 긴 문자열 길이)
- 데이터 저장 시 시간 복잡도 : O(M * L)
- 데이터 조회 시 시간 복잡도 : O(L)
- 문자열 조회시 성능은 좋지만 데이터 저장을 위해 문자 하나하나에 대한 노드가 필요해 많은 메모리 공간이 필요하게 됩니다.
- KMP(Knuth-Morris-Pratt) 알고리즘
- 문자열 탐색 시 불필요하게 모든 문자열을 탐색하는 것이 아니라 필요한 부분에 대해서만 비교할 수 있도록 구현된 알고리즘입니다.
- 비교 과정에서 다른 문자가 발견되면 그 시점에서 접두사와 접미사를 비교해 동일한 문자열 만큼만 점프해 비교를 이어가는 방식입니다.
- 이를 통해, 다를 수 밖에 없는 문자열에 대한 비교를 하지 않고 필요한 부분에 대해서만 비교해 더 나은 효율성을 가질 수 있습니다.
- 시간복잡도는 O(N+M)을 가집니다. (M : 찾고자 하는 문자열 길이 / N : 탐색 대상이 되는 문자열의 길이)
- 전처리 단계(부분 일치 테이블 생성)에서 M만큼의 문자열 조회가 발생합니다.
- 부분일치 테이블을 활용해 N만큼의 문자열을 한번만 조회해 일치하는 데이터를 찾아냅니다.
- 단점은 다음과 같습니다.
- 전처리 단계의 복잡성
- 추가적인 메모리 필요
- 최악의 경우 O(N * M)의 복잡성을 가집니다. -> 결국 모든 문자열에 대한 조회를 해야 하는 경우
- 다른 인코딩 문자에 대한 추가 로직 처리 필요
- Rabin-Karp 알고리즘
- 해시 테이블을 이용해 문자열 탐색을 진행하는 알고리즘 입니다.
- 탐색하고자 하는 문자열의 아스키코드를 가지고 해시를 생성하고 전체 문자열을 순회하면서 해시가 일치하는지 여부만을 확인하는 방식으로 동작합니다.
- 이를 통해 시간 복잡도는 O(N)입니다. (N : 탐색 대상이 되는 문자열의 길이)
- 단점은 다음과 같습니다.
- 충돌로 인한 성능 저하 : 잦은 충돌이 발생할 경우 리스트로 일치여부를 확인해야 하므로 성능이 저하될 수 있다.
- 단일 문자열에 대한 비교만 가능 : 여러개의 문자열을 탐색하기 위해선 그만큼 해시값 생성 및 비교에 대한 소요가 증가해 성능이 저하될 수 있습니다.
하지만 대부분의 경우 해시값이 겹치는 경우는 거의없다.
15. 이진탐색이 무엇인지 설명하고, 시간복잡도를 증명해 보세요.
- 찾고자 하는 값이 나올 때까지 정렬된 배열의 중간값을 기준으로 비교해 탐색범위를 줄어나가는 방식의 틈색 방법입니다.
- 시간 복잡도는 배열의 범위를 1/2로 나눠서 반복하기 때문에 O(Log N)의 복잡도를 가집니다.
Lower Bound, Upper Bound 는 무엇이고, 이를 어떻게 구현할 수 있을까요?
- Lower Bound : 찾는 숫자보다 이상인 숫자가 처음으로 나오는 위치
- 배열의 중간 값(mid)을 가져옵니다.
- 중간 값과 검색 값을 비교합니다.
- 중간 값이 검색 값보다 작다면 left 값을 mid+1로 합니다.
- 중간 값이 검색 값보다 크거나 같다면 right값을 mid로 합니다.
- left ≥ right 일 때까지 1번과 2번을 반복합니다.
- 반복이 끝나면 right 값이 lower bound가 됩니다.
- Upper Bound : 찾는 숫자보다 초과하는 숫자가 처음으로 나오는 위치
- 배열의 중간 값(mid)을 가져옵니다.
- 중간 값과 검색 값을 비교합니다.
- 중간 값이 검색 값보다 작거나 같다면 left 값을 mid+1로 합니다.
- 중간 값이 검색 값보다 크다면 right값을 mid로 합니다.
- left ≥ right 일 때까지 1번과 2번을 반복합니다.
- 반복이 끝나면 right 값이 upper bound가 됩니다.
굳이 두 방식의 의미를 찾아보자면 찾는 값보다 작은 범위를 찾고 싶다면 Lower Bound, 큰 범위를 찾고 싶다면 Upper Bound를 사용하는 것이 가장 정확해서 이지 않을까
이진탐색의 논리를 적용하여 삼진탐색을 작성한다고 가정한다면, 시간복잡도는 어떻게 변화할까요? (실제 존재하는 삼진탐색 알고리즘은 무시하세요!)
- 삼진 탐색의 경우 O(Log N)인 이진 탐색보다 높은 시간 복잡도를 가지게 됩니다. 이론상으로는 O(Log3 N)이 맞지만 더 느린 효율을 보여줍니다.
- 느린 효율을 보여주는 이유는 다음과 같습니다.
- 탐색 범위를 줄여나가기 위해 한번의 연산이 아닌 두번의 연산이 발생한다.
- 이로 인해 탐색 범위가 느리가 줄여져 나가 실제로 찾는 데이터에 도달하는데 더 느린 속도를 가진다.
기존 이진탐색 로직에서 부등호의 범위가 바뀐다면, (ex. <= 라면 <로, <이라면 <= 로) 결과가 달라질까요?
- 구현 방식에 따라 결과가 달라질 수 있습니다.
- Left 와 Right가 같은 경우, 중간값 탐색을 진행할지 안할지에 대한 여부를 선택하는 차이라고 생각합니다.
- 정확한 결과값이 반환되도록 구현하려면 위와 같은 선택을 통해 구현 방식이 달라질 수 있습니다.
- 만약 로직 수정을 하지 않고 부등호의 범위만 변경한다면 의도와는 다른 값이 반환될 수 있습니다.
16. 암호화 알고리즘에 대해 설명해 주세요.
- 암호화 알고리즘은 데이터를 외부로의 노출과 탈취에서 보호하기 위해 데이터를 알아볼 수 없는 암호로 변경하고 해독하는 방식을 의미합니다.
- 대표적인 암호화 알고리즘은 아래와 같이 세 가지 입니다.
- 대칭키 알고리즘
- 클라이언트와 서버가 모두 같은 형태의 키를 가지고 데이터를 암호, 복호화를 하는 방식을 의미합니다.
- 공개키에 비해 빠르고 효율적인 방법이지만 대칭키가 제 3자로부터 탈취된 경우 데이터가 노출될 위험이 높습니다.
- 주요 알고리즘 종류 : DES, AES
- 비대칭키(공개키) 알고리즘
- 공개되지 않는 개인키와 공개되도 상관없는 공개키로 구분해 암호화와 복호화를 진행하는 방식을 의미합니다.
- 개인키로는 복호화, 공개키로는 암호화가 가능합니다.
- 대칭키에 비해 보안적인 측면에서 강력한 효과를 가져올 수 있지만 과정 자체가 복잡해 더 많은 리소스를 필요로 합니다.
- 주요 알고리즘 종류 : DSA, RES, ECC
- 단방향 알고리즘(Hash 알고리즘)
- 해싱을 통해 데이터를 암호화 하는 방식을 의미합니다.
- 데이터의 진위 여부는 알고 싶지만 복호화는 불필요한 경우 사용하는 알고리즘입니다.
- 즉, 암호화는 가능하지만 복호화는 불가능합니다.
- 주요 알고리즘 종류 : SHA-XXX(MD 길이에 따라 상이)
- 대칭키 알고리즘
17. 그리디 알고리즘과 동적 계획법을 비교해 주세요.
- 그리디 알고리즘은 선택의 순간마다 최적의 선택만을 하면서 당장의 최적해를 구하는 방식을 의미합니다.
- 최적의 선택을 탐욕적인 선택이라고도 할 수 있습니다.
빠른 속도로 문제를 처리하는 것이 장점이지만 전체 선택지로 봤을 때, 최적의 선택을 보장하지 않습니다.
- 동적 계획법은 하나의 문제를 작은 부분 문제로 나눠서 해결해 나가는 방식을 의미합니다.
- 중요한 건 작은 부분에 대한 해답을 별도의 저장공간에 저장하고 점차 큰 문제로 해결해 나갈 때, 이 정보를 사용하는 방식이라는 점입니다.
- 이를 통해 반복적인 계산을 줄이고 이전에 구한 값을 그대로 사용함으로써 알고리즘의 성능을 최적화 할 수 있습니다.
두 방식을 비교하자면
- 그리디의 빠른 속도가 장점이지만 전체에서 가장 최적의 선택을 하고 싶다면 동적 계획법을 선택해야 합니다.
그렇다면, 어떤 경우에 각각의 기법을 사용할 수 있을까요?
- 두 방식 모두 최종 해답이 부분 문제에 대해서도 해답이 되는 경우에 사용해야 합니다.
- 하지만 그리디 알고리즘은 부분 문제간의 해답이 영향을 주지 않는 경우에 사용해야 합니다.(거스름돈)
- 이에 반해 동적 계획법은 영향을 주는 경우에 사용해야 저장한 부분 문제의 해답을 사용할 수 있습니다.(LCS: 최 공통 부분 수열)
그렇다면, 동적 계획법으로 풀 수 있는 모든 문제는 재귀로 변환하여 풀 수 있나요?
- Top-Down의 경우는 재귀와 동적 계획법을 사용해 큰 문제 해결을 위한 작은 문제 호출 방법으로 효율적인 방식을 제공할 수 있습니다.
- 하지만 Down-Top 방식의 경우는 반복문을 통해 작은 문제의 결과값을 메모리제이션하면서 동작하기 때문에 재귀로 변환해서 풀기에는 적합하지 않습니다.
- 불가능하지 않지만 반복문을 포기하고 재귀로 처리할 이유가 없다!